Elucidating Human Brain Connectivity Through Deep Learning and Network Analysis

• Funding: 25K AUD + 1 PhD scholarship (tuition fee + stipend for 3 years), which is equivalent to $254,200 AUD.
• Investigators: Kerri Morgan, Frank Jiang, Julien Ugon, Sergiy Shelyag, Hung Le, Nicholas Parsons, Govinda Poudel, Alex Hocking
  
• Role: Partner Investigator. Design deep learning models
• Abstract: In this project, we have identified local features of the brain network that may contribute to preferred structural pathways that facilitate functional connectivity. The relevance or these features in terms of brain function and physiology has been established by a thorough literature search and expertise of collaborators in neuroscience. These have been used as input to a machine learning program developed to determine their contributions in an algorithm for finding these structural pathways using local knowledge only. A paper based on this work is currently in preparation. We have also completed and submitted a paper on structuralfunctional connectivity.
• Publications: Scientific Reports

This project investigates how decentralized, biologically plausible mechanisms can explain signal communication across the human brain’s structural network — even between regions not directly connected.

🧩 Motivation

The human brain is a complex, decentralized network. While many studies model communication using global metrics (e.g., shortest path, searchlight), these models implicitly assume complete network knowledge — a biologically implausible scenario.

Instead, we explore:

• How biologically motivated local features can guide neural signal propagation.
• Whether decentralized navigation strategies can explain the emergence of global communication efficiency.

🧭 Our Approach

We model communication as a local navigation problem over a structural brain graph. A signal (agent) attempts to reach a target node using only local observations at each step.

Graph Setup

Let the structural connectome be represented as a graph:

with:

• $\mathcal{V}$: nodes (brain regions)
• $\mathcal{E}$: weighted edges (structural connections)

Each communication trial involves:

• A source node $s \in \mathcal{V}$
• A target node $t \in \mathcal{V}$

We simulate a navigation trajectory $\tau = (v_0 = s, v_1, \dots, v_k = t)$ using a local navigating policy.

🧠 RL Formulation of Neural Communication

We frame the pathfinding problem as a Markov Decision Process (MDP):

• State space: $\mathcal{S} = \mathcal{V}$
• Action space: $\mathcal{A}_v = {u \in \mathcal{N}(v)}$ (neighbors of current node $v$)
• Transition: deterministic, next state is $v_{k+1} = a_k=u$ at navigation step $k$
• Policy: $\pi(u \mid v_k, t)$ that determines the next node on the path given current node $v_k$ and target node $t$, defined below
• Reward: $r_k = R(v_k, a_k; t)$, defined below

Objective

The agent aims to maximize path efficiency (e.g., inverse length or success rate), under biologically plausible constraints.

We define a local feature vector:

where:

• $v_k$: current node
• $u \in \mathcal{N}(v_k)$: candidate neighbor
• $t$: target node
• Each component of $\phi$ is a biologically plausible local feature (e.g., whether $u = t$, whether $u$ shares a region with $t$, etc.)

The navigation policy is parameterized as:

where $\theta \in \mathbb{R}^d$ are learned weights governing the importance of each local feature. The RL algorithm learns a navigation policy with different combinations of criteria to compute edge weights. The purpose is to find the combination that maximises the efficiency of the obtained path

Reward Design

We define the reward in terms of navigation efficiency, following prior work (Seguin et al., 2018).

For a pair of nodes $(i, j)$, let:

• $\Lambda_{i,j}$: the length of the path found by the agent.
• $\Lambda_{i,j}^*$: the length of the shortest path between $i$ and $j$ in the structural connectome. This is considered as the “ground-truth” as can be computed using global information available in the training data.

The efficiency ratio of a path is:

This value lies in ( (0, 1] ), where 1 corresponds to shortest-path optimality.

We use this efficiency as a reward signal for training navigation policies. The cumulative reward for a trajectory $\tau$ is:

where:

• $E^F$ are the pairs of nodes in the structural connectome which are functionally connected
• $|E^F|$ is the number of those pairs.

🔧 Optimization

We treat the task as a reinforcement learning to maximize expected cumulative reward:

Gradients are computed using REINFORCE:

where $R(\tau)$ is the total return of the trajectory.

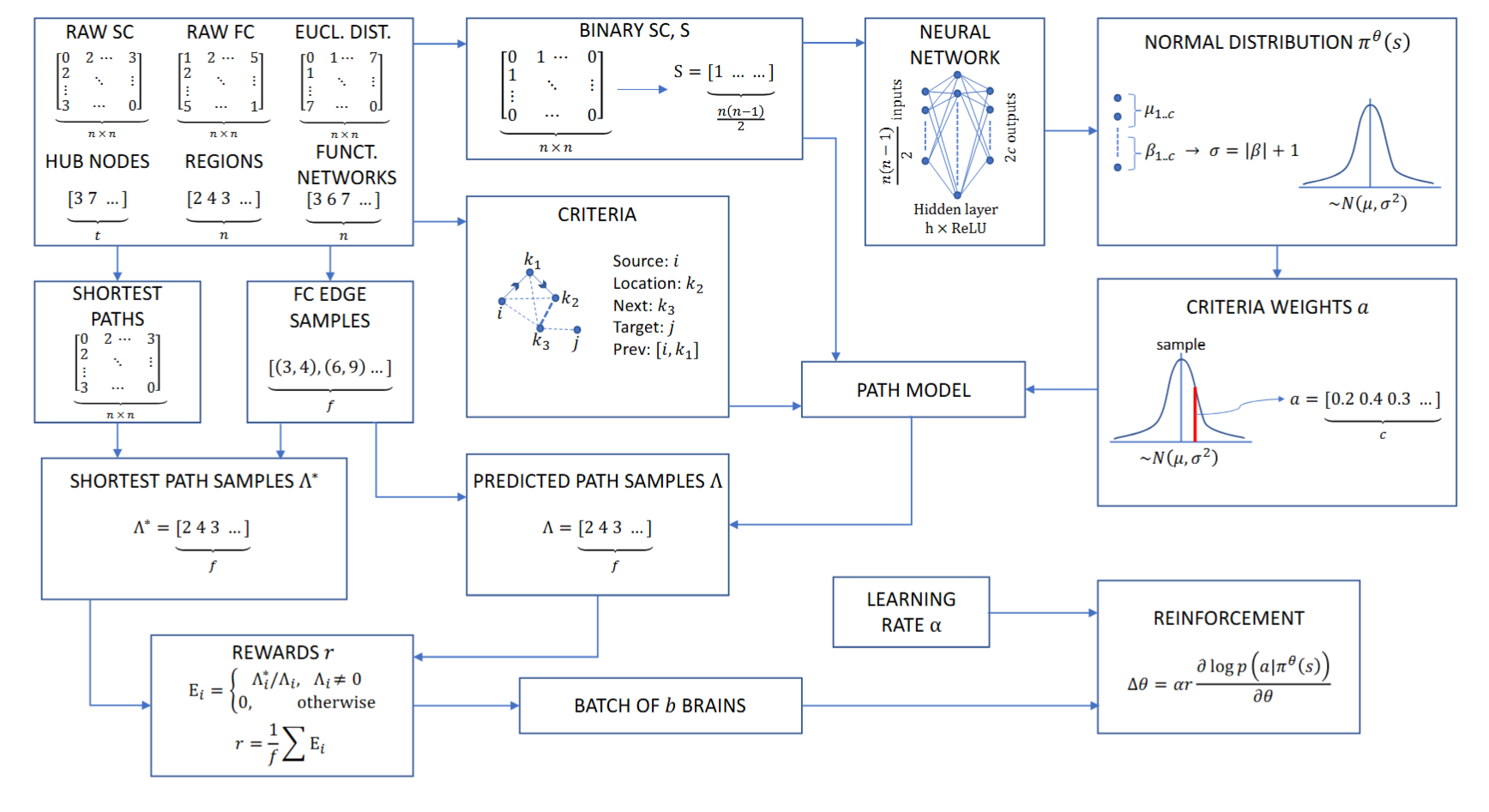
Brain Path Finding Framework Using RL.

📊 Results Summary

• Our locally optimized policy nearly matches global methods in reachability and communication efficiency.
• Policies learn to prioritize biologically plausible features such as region membership and inter-areal edges.

In particular, the RL navigation algorithm was trained on 100 human structural-functional connectome pairs to maximize average navigation efficiency above. Across 30,000 iterations per brain, the model sampled 100 functionally connected node pairs per step, optimizing over 300 million pairwise samples. The learned navigation policy assigns weighted scores to neighboring nodes based on four binary criteria (e.g., proximity to target region, interregional connection), with weights indicating their relative importance. The model achieved a 100% success rate in connecting functionally linked nodes, with an average efficiency of 83.8% (min: 72.3%, median: 83.9%), and most connectomes exhibiting efficiency between 80–90%.

References

C. Seguin,M.P. van den Heuvel,& A. Zalesky, Navigation of brain networks, Proc. Natl. Acad. Sci. U.S.A. 115 (24) 6297-6302, https://doi.org/10.1073/pnas.1801351115 (2018).