Program Memory: Method (part 2)
Published:
When a human programmer codes, he often uses core libraries to construct his programs. Most of the time, the program memory stores these static libraries, and let big programs be created dynamically during computation. The libraries are unitary components constructing bigger programs. Maintaining small and functionally independent sub-programs such as libraries encourage program utilisations since an immense program must refer to different libraries to complete its task. Indeed, it also eliminates redundancies as the stored programs-the core libraries are not overlapping each other.
Singular Programs
In a recent paper [1], we invent an efficient program memory that stores elementary, sharable, and small programs called singular programs. A standard program can be composed of singular programs using low-rank approximation (SVD):
\[\mathbf{P}=\sum_{n}^{r_{m}}\sigma_{n}u_{n}v_{n}^{\top}\tag{1}\]where $\sigma_n,u_n$ and $v_n$ are singular programs (in vector form) retrieved from the program memory $M_p={\mathbf{M_U,M_V,M_S}}$.
Here, $\mathbf{M_U}$ and $\mathbf{M_V}$ are the matrices whose rows are singular vector programs ($u,v$) and $\mathbf{M_S}$ is a vector containing singular value programs ($\sigma$). Similar to NSM, the retrieval of these singular programs is done via attention. The only note is we need to ensure $\sigma_{1}>\sigma_{2}>…>\sigma_{r_m}>0$ during retrieval. Hence, we normalize the attention results as:
\[\sigma_{n}=\begin{cases} \mathbf{softplus}\left(\sum_{i=1}^{P_{s}}w_{in}^{\sigma}\mathbf{M_S}\left(i\right)\right) & n=r_{m}\\ \sigma_{n+1}+\mathbf{softplus}\left(\sum_{i=1}^{P_{s}}w_{in}^{\sigma}\mathbf{M_S}\left(i\right)\right) & n<r_{m} \end{cases}\tag{2}\]where $w^{\sigma}_{in}$ is the attention weight for $i$-th slot in $\mathbf{M_S}$ in the $n$-th component. For singular vectors, the attentional retrieval is simple:
\[u_{n}=\sum_{i=1}^{P_{u}}w_{in}^{u}\mathbf{M_U}\left(i\right)\qquad v_{n}=\sum_{i=1}^{P_{v}}w_{in}^{v}\mathbf{M_V}\left(i\right)\tag{3}\]Unlike those in NSM, the singular programs here are much smaller, which allows efficient manipulation to create sophisticated memory reading.
Orthogonal constraint. Simulating unitary functions, singular programs are supposed to be orthogonal in their representation space. In particular, we enforce unitary properties by minimizing
\[\mathcal{L}_{o}=\left\Vert \mathbf{M_U}\mathbf{M_U}^{\top}-\mathbf{I}+\mathbf{M_V}\mathbf{M_V}^{\top}-\mathbf{I}\right\Vert _{2}\tag{4}\]Recurrent attention. A straightforward retrieval will execute $r_m$ attentions in parallel and read $\sigma_n,u_n$ and $v_n$ independently. Another option is to carry out the attention step-by-step and component-by-component using a recurrent program controller. Doing so enables the attention process of the past components to determine the current component attention. Being aware of the past attention makes avoiding program collapse possible, as the model just needs to attend differently from the past. Another benefit of recurrent attention is to make the whole attention process more consistent, targeting a long-term goal to generate the optimal sequence of singular components that best represent the working program.
Using programs by knowing their names. While the vanilla NSM uses identifiers to differentiate programs, the Neurocoder refers to programs by “names”. Intuitively, a name carries certain information on the function of a program. For example, the name quick_sort() reveals the algorithm that the program uses to sort. To realise this idea, we can use a neural network to compress the content of the singular program into a low-dimension vector (key or name). The key will represent the program in performing attention.
General-purpose computation
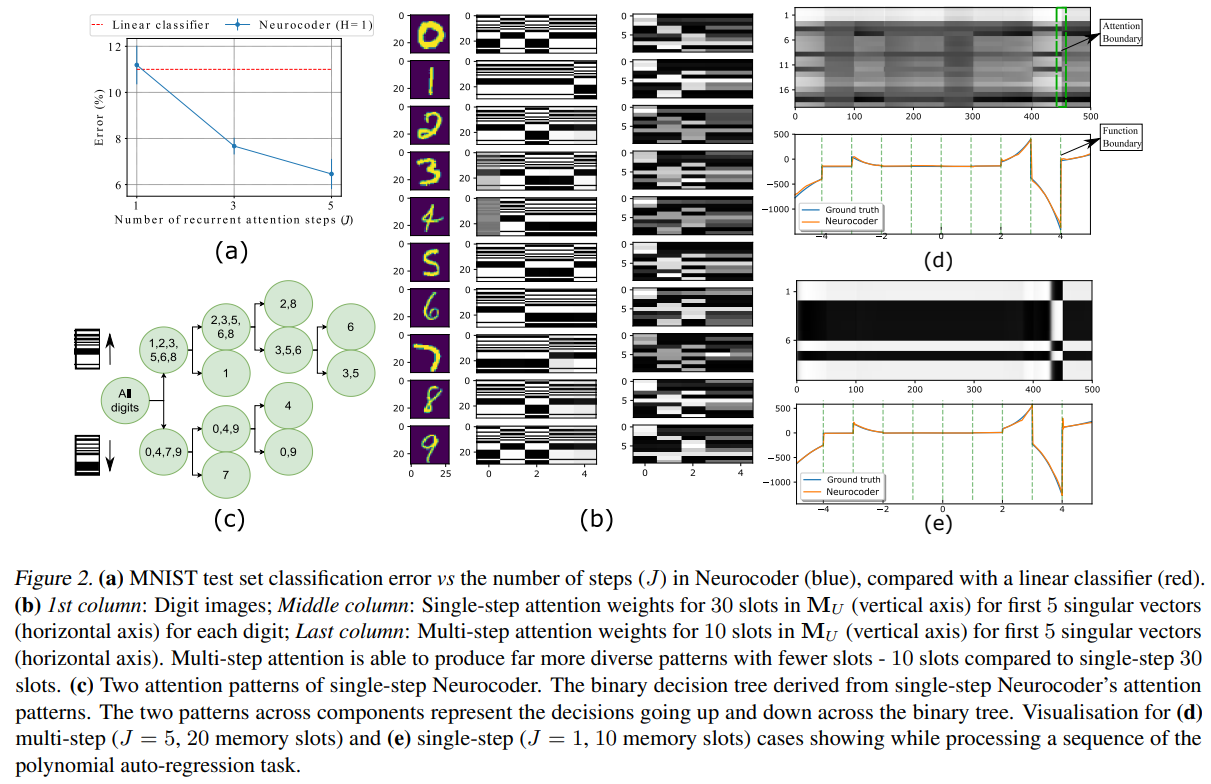
Neurocoder shows remarkable adaptive computing ability as shown in Fig. 2. The attention patterns change over components and resemble a binary-tree decision-making process. With recurrent attention, program collapse is annihilated and the program changes as the input distribution shifts.
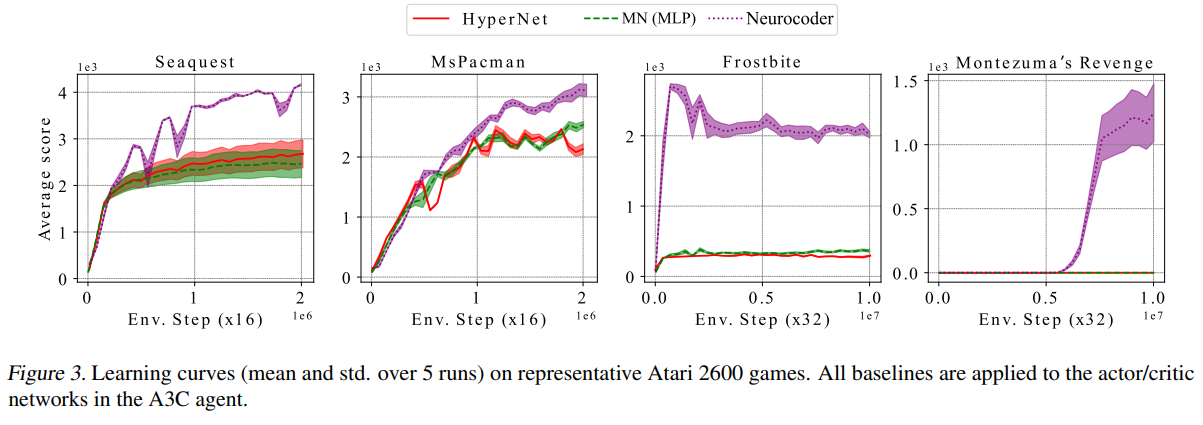
In reinforcement learning, Neurocoder-empowered agents can learn faster and even break the learning bottleneck of other methods in the notorious Atari games like Montezuma’s Revenge (Fig. 3). Neurocoder helps because it composes different policy programs in response to state changes. For example, the agent moves to a different room/level using different skills to walk through successfully (e.g. climb the ladder in the ladder room and jump over snakes in the snake room). Notably, another adaptive computing model like HyperNet [2] fails to help the agent to learn. The key difference here is singular program is sharable, leading to policy programs that reuse skills. It is modular and goes beyond adaptation.
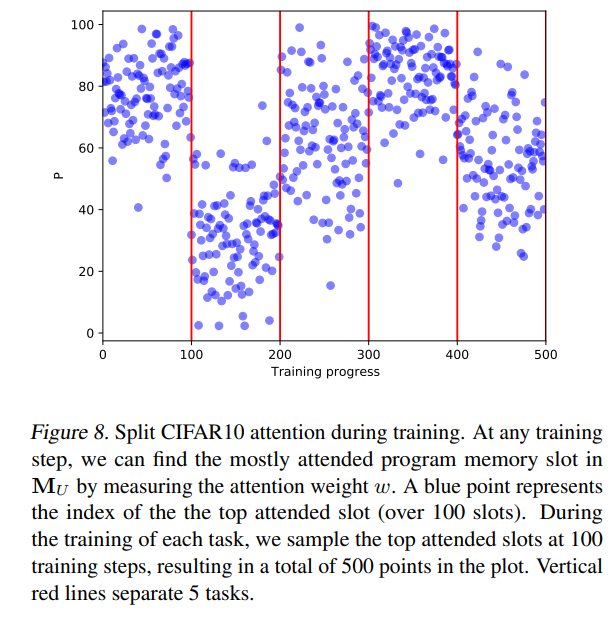
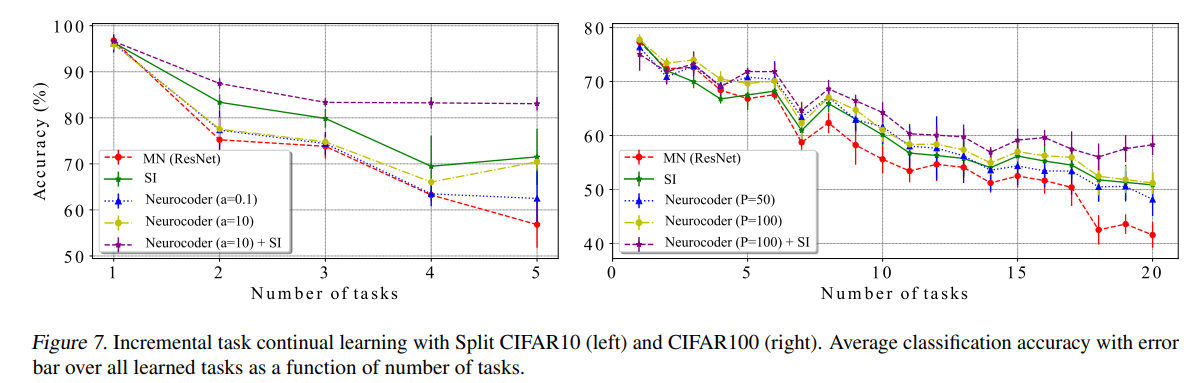
In continual learning, Neurocoder helps overcome catastrophic forgetting by assigning different programs to different tasks (Fig. 8). Learning over 5 or 20 tasks shows less degradation with Neurocoder (Fig. 7). Ablation studies indicate more programs and orthogonal enforcement are beneficial.
Where next
Neurocoder makes storing efficient programs possible and supports dynamic program creation. However, it does not support dynamic program editing. After training, the program memory is read-only, making it more like a ROM, storing hard libraries in embedded systems. A fully flexible program memory system needs mechanisms to update the program during inference, replace or delete programs based on current input data. Another open problem is to interpret the meaning of the stored programs. What are the instructions carried by these programs? Are they transferable? Future works will find the answers.
Reference
[1] Le, Hung, and Svetha Venkatesh. “Neurocoder: General-purpose computation using stored neural programs.”In ICML (2022).
[2] Ha, David, Andrew Dai, and Quoc V. Le. “Hypernetworks.” arXiv preprint arXiv:1609.09106 (2016).
